Structure-Aware Spectral Sparsification via Uniform Edge Sampling

Spectral clustering is a fundamental method for graph partitioning, but its reliance on eigenvector computation limits scalability to massive graphs. Classical sparsification methods preserve spectral properties by sampling edges proportionally to their effective resistances, but require expensive preprocessing to estimate these resistances. We study whether uniform edge sampling-a simple, structure-agnostic strategy-can suffice for spectral clustering. Our main result shows that for graphs admitting a well-separated $k$-clustering, characterized by a large structure ratio $\Upsilon(k) = \lambda_{k+1} / \rho_G(k)$, uniform sampling preserves the spectral subspace used for clustering. Specifically, we prove that uniformly sampling $O(\gamma^2 n \log n / \epsilon^2)$ edges, where $\gamma$ is the Laplacian condition number, yields a sparsifier whose top $(n-k)$-dimensional eigenspace is approximately orthogonal to the cluster indicators. This ensures that the spectral embedding remains faithful, and clustering quality is preserved. Our analysis introduces new resistance bounds for intra-cluster edges, a rank-$(n-k)$ effective resistance formulation, and a matrix Chernoff bound adapted to the dominant eigenspace. These tools allow us to bypass importance sampling entirely. Conceptually, our result connects recent coreset-based clustering theory to spectral sparsification, showing that under strong clusterability, even uniform sampling is structure-aware. This provides the first provable guarantee that uniform edge sampling suffices for structure-preserving spectral clustering.

Topological Signatures of ReLU Neural Network Activation Patterns

This paper explores the topological signatures of ReLU neural network activation patterns. We consider feedforward neural networks with ReLU activation functions and analyze the polytope decomposition of the feature space induced by the network. Mainly, we investigate how the Fiedler partition of the dual graph and show that it appears to correlate with the decision boundary -- in the case of binary classification. Additionally, we compute the homology of the cellular decomposition -- in a regression task -- to draw similar patterns in behavior between the training loss and polyhedral cell-count, as the model is trained.

Surrogate Graph Partitioning for Spatial Prediction

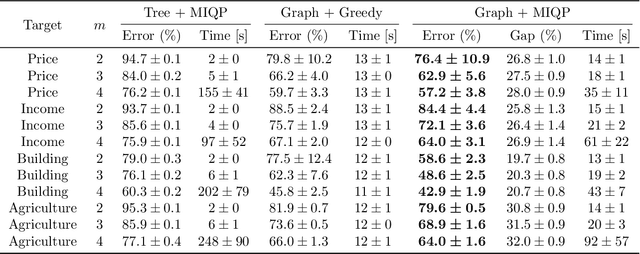
Spatial prediction refers to the estimation of unobserved values from spatially distributed observations. Although recent advances have improved the capacity to model diverse observation types, adoption in practice remains limited in industries that demand interpretability. To mitigate this gap, surrogate models that explain black-box predictors provide a promising path toward interpretable decision making. In this study, we propose a graph partitioning problem to construct spatial segments that minimize the sum of within-segment variances of individual predictions. The assignment of data points to segments can be formulated as a mixed-integer quadratic programming problem. While this formulation potentially enables the identification of exact segments, its computational complexity becomes prohibitive as the number of data points increases. Motivated by this challenge, we develop an approximation scheme that leverages the structural properties of graph partitioning. Experimental results demonstrate the computational efficiency of this approximation in identifying spatial segments.

BioBlobs: Differentiable Graph Partitioning for Protein Representation Learning

Protein function is driven by coherent substructures which vary in size and topology, yet current protein representation learning models (PRL) distort these signals by relying on rigid substructures such as k-hop and fixed radius neighbourhoods. We introduce BioBlobs, a plug-and-play, fully differentiable module that represents proteins by dynamically partitioning structures into flexibly-sized, non-overlapping substructures ("blobs"). The resulting blobs are quantized into a shared and interpretable codebook, yielding a discrete vocabulary of function-relevant protein substructures used to compute protein embeddings. We show that BioBlobs representations improve the performance of widely used protein encoders such as GVP-GNN across various PRL tasks. Our approach highlights the value of architectures that directly capture function-relevant protein substructures, enabling both improved predictive performance and mechanistic insight into protein function.

InfraredGP: Efficient Graph Partitioning via Spectral Graph Neural Networks with Negative Corrections

Graph partitioning (GP), a.k.a. community detection, is a classic problem that divides nodes of a graph into densely-connected blocks. From a perspective of graph signal processing, we find that graph Laplacian with a negative correction can derive graph frequencies beyond the conventional range $[0, 2]$. To explore whether the low-frequency information beyond this range can encode more informative properties about community structures, we propose InfraredGP. It (\romannumeral1) adopts a spectral GNN as its backbone combined with low-pass filters and a negative correction mechanism, (\romannumeral2) only feeds random inputs to this backbone, (\romannumeral3) derives graph embeddings via one feed-forward propagation (FFP) without any training, and (\romannumeral4) obtains feasible GP results by feeding the derived embeddings to BIRCH. Surprisingly, our experiments demonstrate that based solely on the negative correction mechanism that amplifies low-frequency information beyond $[0, 2]$, InfraredGP can derive distinguishable embeddings for some standard clustering modules (e.g., BIRCH) and obtain high-quality results for GP without any training. Following the IEEE HPEC Graph Challenge benchmark, we evaluate InfraredGP for both static and streaming GP, where InfraredGP can achieve much better efficiency (e.g., 16x-23x faster) and competitive quality over various baselines. We have made our code public at https://github.com/KuroginQin/InfraredGP

Toward Quantum Utility in Finance: A Robust Data-Driven Algorithm for Asset Clustering

Clustering financial assets based on return correlations is a fundamental task in portfolio optimization and statistical arbitrage. However, classical clustering methods often fall short when dealing with signed correlation structures, typically requiring lossy transformations and heuristic assumptions such as a fixed number of clusters. In this work, we apply the Graph-based Coalition Structure Generation algorithm (GCS-Q) to directly cluster signed, weighted graphs without relying on such transformations. GCS-Q formulates each partitioning step as a QUBO problem, enabling it to leverage quantum annealing for efficient exploration of exponentially large solution spaces. We validate our approach on both synthetic and real-world financial data, benchmarking against state-of-the-art classical algorithms such as SPONGE and k-Medoids. Our experiments demonstrate that GCS-Q consistently achieves higher clustering quality, as measured by Adjusted Rand Index and structural balance penalties, while dynamically determining the number of clusters. These results highlight the practical utility of near-term quantum computing for graph-based unsupervised learning in financial applications.

Towards Explainable Job Title Matching: Leveraging Semantic Textual Relatedness and Knowledge Graphs

Semantic Textual Relatedness (STR) captures nuanced relationships between texts that extend beyond superficial lexical similarity. In this study, we investigate STR in the context of job title matching - a key challenge in resume recommendation systems, where overlapping terms are often limited or misleading. We introduce a self-supervised hybrid architecture that combines dense sentence embeddings with domain-specific Knowledge Graphs (KGs) to improve both semantic alignment and explainability. Unlike previous work that evaluated models on aggregate performance, our approach emphasizes data stratification by partitioning the STR score continuum into distinct regions: low, medium, and high semantic relatedness. This stratified evaluation enables a fine-grained analysis of model performance across semantically meaningful subspaces. We evaluate several embedding models, both with and without KG integration via graph neural networks. The results show that fine-tuned SBERT models augmented with KGs produce consistent improvements in the high-STR region, where the RMSE is reduced by 25% over strong baselines. Our findings highlight not only the benefits of combining KGs with text embeddings, but also the importance of regional performance analysis in understanding model behavior. This granular approach reveals strengths and weaknesses hidden by global metrics, and supports more targeted model selection for use in Human Resources (HR) systems and applications where fairness, explainability, and contextual matching are essential.

Research on Multi-hop Inference Optimization of LLM Based on MQUAKE Framework

Accurately answering complex questions has consistently been a significant challenge for Large Language Models (LLMs). To address this, this paper proposes a multi-hop question decomposition method for complex questions, building upon research within the MQUAKE framework. Utilizing the LLAMA3 model, we systematically investigate the impact of multi-hop question decomposition within knowledge graphs on model comprehension and reasoning accuracy, both before and after model training. In our experiments, we systematically partitioned and converted the MQUAKE-T dataset into two distinct formats: a single-hop dataset designed for directly answering complex questions, and a multi-hop dataset constructed using the multi-hop question decomposition method. We then fine-tuned the LLAMA3 model on these datasets and conducted inference tests. Our results demonstrate that, without fine-tuning the LLM, the prediction performance based on the multi-hop question decomposition method significantly outperforms the method of directly answering complex questions. After fine-tuning using the LoRA (Low-Rank Adaptation) method, the performance of both approaches improved compared to the untrained baseline. Crucially, the method utilizing multi-hop decomposition consistently maintained its superiority. These findings validate the effectiveness of the multi-hop decomposition method both before and after training, demonstrating its capability to effectively enhance the LLM's ability to answer complex questions.

Graph-Based Feature Augmentation for Predictive Tasks on Relational Datasets

Data has become a foundational asset driving innovation across domains such as finance, healthcare, and e-commerce. In these areas, predictive modeling over relational tables is commonly employed, with increasing emphasis on reducing manual effort through automated machine learning (AutoML) techniques. This raises an interesting question: can feature augmentation itself be automated and identify and utilize task-related relational signals? To address this challenge, we propose an end-to-end automated feature augmentation framework, ReCoGNN, which enhances initial datasets using features extracted from multiple relational tables to support predictive tasks. ReCoGNN first captures semantic dependencies within each table by modeling intra-table attribute relationships, enabling it to partition tables into structured, semantically coherent segments. It then constructs a heterogeneous weighted graph that represents inter-row relationships across all segments. Finally, ReCoGNN leverages message-passing graph neural networks to propagate information through the graph, guiding feature selection and augmenting the original dataset. Extensive experiments conducted on ten real-life and synthetic datasets demonstrate that ReCoGNN consistently outperforms existing methods on both classification and regression tasks.

Weisfeiler-Lehman meets Events: An Expressivity Analysis for Continuous-Time Dynamic Graph Neural Networks

Graph Neural Networks (GNNs) are known to match the distinguishing power of the 1-Weisfeiler-Lehman (1-WL) test, and the resulting partitions coincide with the unfolding tree equivalence classes of graphs. Preserving this equivalence, GNNs can universally approximate any target function on graphs in probability up to any precision. However, these results are limited to attributed discrete-dynamic graphs represented as sequences of connected graph snapshots. Real-world systems, such as communication networks, financial transaction networks, and molecular interactions, evolve asynchronously and may split into disconnected components. In this paper, we extend the theory of attributed discrete-dynamic graphs to attributed continuous-time dynamic graphs with arbitrary connectivity. To this end, we introduce a continuous-time dynamic 1-WL test, prove its equivalence to continuous-time dynamic unfolding trees, and identify a class of continuous-time dynamic GNNs (CGNNs) based on discrete-dynamic GNN architectures that retain both distinguishing power and universal approximation guarantees. Our constructive proofs further yield practical design guidelines, emphasizing a compact and expressive CGNN architecture with piece-wise continuously differentiable temporal functions to process asynchronous, disconnected graphs.